Mathematical definitions

Notations and basic modeling

Notations

First, let us define main quantities of interest involved in EPR imaging in the continuous setting (we shall use the superscript ‘\(c\)’ to designate continuous signals and differentiate them from their discrete counterparts). For the sake of simplicity, we consider that the sample to be imaged is made of a single paramagnetic species X (more specific notations will be introduced when dealing with multiple EPR sources). Let

\(h_X^c : \mathbb{R} \to \mathbb{R}\) be the reference spectrum (also known as zero-gradient spectrum) of the paramagnetic species X;
\(U_X^c : \mathbb{R}^d \to \mathbb{R}\) be the concentration mapping of the paramagnetic species X (where \(d \in \{2,3\}\) denotes the dimension of the spatial domain).

Now, let us consider that a field gradient \(\gamma \in \mathbb{R}^d\) is applied inside the EPR resonator. Let \(\mu = \|\gamma\| \in \mathbb{R}_+\) be the magnitude of the field gradient, and let us denote by \(e_\theta \in \mathbb{R}^d\) the unit vector of the sphere such that

\[\gamma = \mu \cdot e_\theta \,.\]

The parameter \(\theta\in\mathbb{R}^{d-1}\) is an angular parameter that characterizes the orientation \(e_\theta\) of the field gradient \(\gamma\). In practice, when \(d=2\), the parameter \(\theta \in \mathbb{R}\) corresponds to the angle of the polar coordinate system, and when \(d=3\), the parameter \(\theta = (\theta_1, \theta_2) \in \mathbb{R}^2\) is made of the longitudinal (\(\theta_1\)) and latitudinal (\(\theta_2\)) angles of the spherical coordinate system.

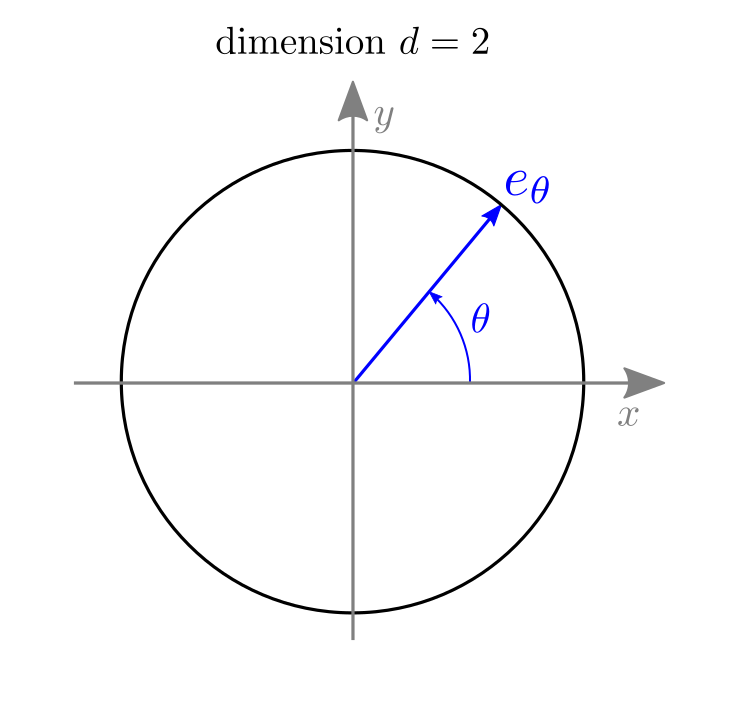
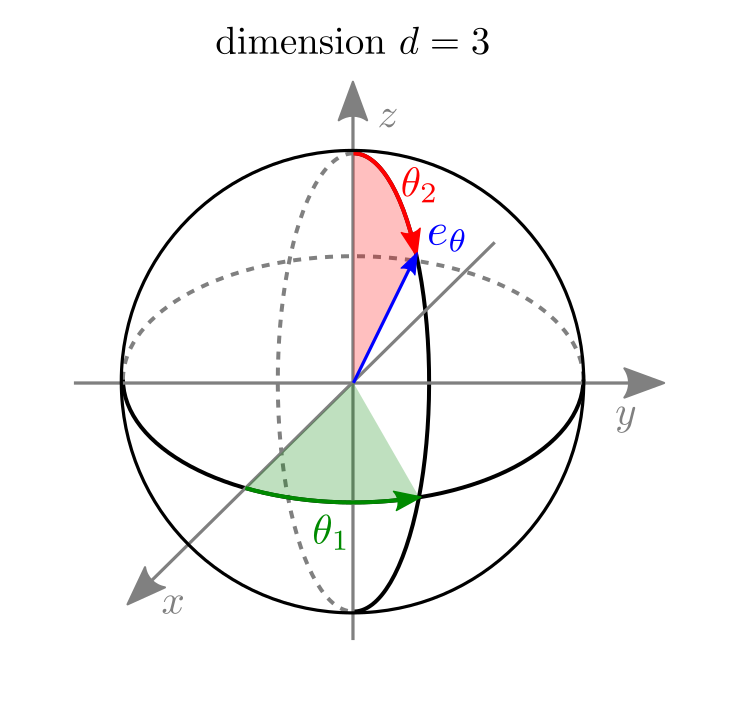
Notice that, in this modeling, the continuous signals \(h_X^c\) and \(U_X^c\) were extended by zero outside from their actual supports (leading to a signal \(h_X^c\) defined over \(\mathbb{R}\) and a signal \(U_X^c\) defined over \(\mathbb{R}^d\)) in order to facilitate their continuous description using standard operators (convolution, Fourier transform, Radon transform, etc.). The domains of those signals will be restricted back to a finite domain when we will define their discrete counterparts.

Radon transform

In the following, we will denote by \(\mathcal{R}_\theta(U_X^c) : \mathbb{R}\to \mathbb{R}\) the Radon transform of \(U_X^c\) in the direction \(e_\theta\), which is defined by

(1)\[\forall r \in \mathbb{R}\,,\quad \mathcal{R}_\theta(U_X^c)(r) = \int_{\mathrm{Span(e_\theta)^\perp}} U_X^c(r e_\theta + s) \, \mathrm{d}s = \int_{\mathbb{R}^d} U_X^c(x) \, \delta_*(\langle x, e_\theta \rangle - r) \, \mathrm{d}x\,,\]

where \(\langle \cdot, \cdot \rangle\) denotes the canonical inner product in \(\mathbb{R}^d\) and \(\delta_*(\cdot)\) denotes the Dirac mass. The Radon transform is at the core of the modeling of EPR imaging, as we shall see below.

Projections and sinograms

An EPR projection corresponds to the mono-dimensional signal \(\mathcal{P}_{X,\gamma}^c : \mathbb{R} \to \mathbb{R}\), acquired when ramping up the intensity \(B \in \mathbb{R}\) of the homogeneous magnetic field applied to the paramagnetic sample (in presence of a field gradient \(\gamma\)). An EPR projection can be linked to the reference spectrum \(h_X^c\) of the EPR species contained in the sample and its concentration mapping \(U_X^c\) through the relation

(2)\[\forall B \in \mathbb{R}\,,\quad \mathcal{P}_{X,\gamma}^{c}(B) = \big(h_X^c * \mathcal{R}_\theta^{\mu}(U_X^c)\big)(B) := \int_{\mathbb{R}} h_X^c(B') \cdot \mathcal{R}_\theta^\mu(U_X^c)(B-B') \, \mathrm{d}B'\,,\]

where \(*\) denotes the convolution operator and \(\mathcal{R}_\theta^\mu(U_X^c)\) denotes the dilatation of the Radon transform of \(U_X^c\) by the factor \(-\mu\) (recall that \(\mu = \|\gamma\|\) represents the magnitude of the field gradient \(\gamma\)), which is defined by

(3)\[\forall B \in \mathbb{R}\,,\quad \mathcal{R}_\theta^\mu(U_X^c)(B) = \frac{1}{\mu} \cdot \mathcal{R}_\theta(U_X^c)(-B/\mu)\,.\]

An EPR sinogram simply corresponds to the aggregation of multiple projections, acquired for different values of field gradient \(\gamma\) (i.e., different values of orientation \(e_\theta\) or/and magnitude \(\mu\)). Given a sequence \(\Gamma = (\gamma_1, \gamma_2, \dots, \gamma_N) \in (\mathbb{R}^d)^N\) made of \(N\) magnetic field gradient vectors, a sinogram \(\mathcal{S}_{\Gamma}^c\) can be defined as

(4)\[\forall B \in \mathbb{R} \,,\quad \mathcal{S}_{X,\Gamma}^c(B) = \big( \mathcal{P}_{X,\gamma_1}^c(B), \mathcal{P}_{X,\gamma_2}^c(B), \dots, \mathcal{P}_{X,\gamma_N}^c(B) \big)\,.\]

In most commercial EPR-imagers, a sinogram corresponds to the acquisition of multiple projections with a fixed field gradient intensity \(\mu\) and multiple field gradient orientations \(e_\theta\). However, we will not limit to this particular situation and consider that a sinogram can gather projections acquired with different field gradient \(\gamma\), without any supplementary assumption.

Discretization

In practice, the acquired spectra, projections and the images that we reconstruct are discrete signals with finite number of samples. We shall explain now how those signals can be linked to their continuous counterparts. In the next sections, we will focus on the definitions of the discrete projection / backprojection operators implemented in the PyEPRI package.

First, let us introduce a generic (and useful) notation to refer to the domain of the discrete signals. For any integer \(K>0\) (representing a number of sample), we denote by \(I_K\) the set of \(K\) consecutive integers centered at 0, defined by

(5)\[I_K = \left[-\frac{K}{2}, \frac{K}{2}\right) \cap \mathbb{Z} = -\left\lfloor \frac{K}{2} \right\rfloor + \bigg\{0, 1, \dots, K-1\bigg\},\]

where \(\lfloor \cdot \rfloor\) denotes the lower integer part operator.

In practice, EPR spectra and projections are not acquired for all \(B \in \mathbb{R}\) but over a bounded acquisition range of homogeneous magnetic field intensity,

(6)\[B \in B_{cf} + \left[- \frac{B_{sw}}{2} \,,\, \frac{B_{sw}}{2} \right],\]

where \(B_{cf} \in \mathbb{R}\) and \(B_{sw} \in \mathbb{R}_+\) are called the center-field and the sweep-width and respectively represent the center and the length of this acquisition range. During an EPR experiment, we consider that all acquired projections share the same acquisition range defined by (6). Real-life acquisitions are made for a finite number of samples of homogeneous magnetic field intensities in the acquisition range. We will assume those samples to be regularly spaced. Let us denote by \(N_B\) the number of samples, the homogeneous magnetic field intensity nodes are the \(\{B_m\}_{m \in I_{N_B}}\) defined by

(7)\[\forall m \in I_{N_B}, \quad B_m = B_{cf} + m \cdot \delta_B\,.\]

where \(\delta_B = \tfrac{B_{sw}}{N_B}\) represents the sampling step of the homogeneous magnetic field intensity.

Accurate sampling always come after an appropriate filtering and we will place ourselves in this setting (see more details in [ABDF23]). For that purpose, we introduce below the filtered reference spectrum \(\widetilde{h_X^c}: \mathbb{R} \to \mathbb{R}\) and projection \(\widetilde{\mathcal{P}_{X,\gamma}^c}\) defined by

(8)\[\widetilde{h_X^c} = g_{\delta_B} * h_X^c \quad \text{and} \quad \widetilde{\mathcal{P}_{X,\gamma}^c} = g_{\delta_B} * \mathcal{P}_{X,\gamma}^c\,,\]

where \(g_{\delta_B}\) is the cut-band filter defined through its Fourier transform

(9)\[\begin{split}\forall \xi \in \mathbb{R}\,,\quad \mathcal{F}(g_{\delta_B}) = \int_{\mathbb{R}} g_{\delta_B}(B) \, e^{-i B\xi} \, \mathrm{d}B = \left\{\begin{array}{cl}1 & \text{if } |\xi| \leq \frac{\pi}{\delta_B}\\ 0 & \text{otherwise.}\end{array}\right.\end{split}\]

A direct consequence from (8) is that the Fourier transform of the filtered signal \(\widetilde{h_X^c}\) (respectively \(\widetilde{\mathcal{P}_{X,\gamma}^c}\)) coincides with that of \(h_X^c\) (respectively \({\mathcal{P}_{X,\gamma}^c}\)) over the frequency domain \(\left[-\frac{\pi}{\delta_B}, \frac{\pi}{\delta_B}\right]\) and is zero outside from this domain. In practice, the fast decrease of the Fourier transforms of \(h_X^c\) and \(\mathcal{P}_{X,\gamma}^c\) (both quickly fall below the noise level) allows to consider that \(\widetilde{h_{X}^c} \approx h_{X}^c\) and \(\widetilde{\mathcal{P}_{X,\gamma}^c} \approx \mathcal{P}_{X,\gamma}^c\) and as long as the sampling step \(\delta_B\) is small enough.

Now we are ready to define the discrete counterparts of the continuous signals \(h_X^c\) and \(\mathcal{P}_{X,\gamma}^c\) (projection acquired in presence of a field gradient \(\gamma\)). We will denote those counterparts by \(h_X^\mathrm{d} : I_{N_B} \mapsto \mathbb{R}\) and \(p_{X,\gamma} : I_{N_B} \mapsto \mathbb{R}\). Those discrete and finite signals are defined by

(10)\[\forall m \in I_{N_B}\,,\quad h_X(m) = \widetilde{h_X^c}(B_m) \quad \text{and} \quad p_{X,\gamma}(m) = \widetilde{\mathcal{P}_{X,\gamma}^c}(B_m)\,.\]

We shall introduce now the sampling of \(U_X^c\) over a regular grid. Let \(\delta > 0\) be a spatial sampling step (this spatial sampling step is common to all coordinate axes of the image and will be in practice set by the user of image reconstruction algorithms). Again, we need to introduce the filtering of the image \(U_X^c\) into \(\widetilde{U_X^c} = f_\delta * U_X^c\) where the cut-band filter \(f_\delta\) is defined through its Fourier transform by

(11)\[\begin{split}\forall \xi \in \mathbb{R}^d\,,\quad \mathcal{F}(f_\delta)(\xi) = \int_{\mathbb{R}^d} f_\delta(x) \, e^{-i \langle x, \xi \rangle} \, \mathrm{d} x = \left\{\begin{array}{cl}1 &\text{if } \|\xi\| \leq \frac{\pi}{\delta}\\ 0 &\text{otherwise.}\end{array}\right.\end{split}\]

Now, let \((N_i)_{1 \leq i \leq d}\) be the numbers of samples along the \(d\) coordinate axes of the sampled image, let \(\Omega = I_{N_1} \times \dots \times I_{N_d}\), and let \(u_X : \Omega \to \mathbb{R}\) be the discrete image defined by

(12)\[\forall k \in \Omega\,,\quad u_X(k) = \widetilde{U_X^c}(k \delta)\,.\]

Before going further, let us recall the definition of the discrete Fourier transform of a (mono-dimensional) discrete signal. Given any discrete signal \(v : I_{N_B} \to \mathbb{R}\), we call discrete Fourier transform of \(v\) the (\(N_B\)-periodical) discrete and complex signal \(\mathrm{DFT}(v) : \mathbb{Z} \to \mathbb{C}\) defined by

(13)\[\forall \alpha \in \mathbb{Z}\,,\quad \mathrm{DFT}(v)(\alpha) = \sum_{m \in I_{N_B}} v(m) \, e^{-2 i \pi m \alpha/N_B}\,.\]

The \(\mathrm{DFT}\) operator is invertible and we shall denote by \(\mathrm{IDFT}\) its inverse. The \(\mathrm{DFT}\) and \(\mathrm{IDFT}\) operators can be efficiently evaluated using the Fast Fourier Transform (FFT) Algorithm, in particular, using the Fastest Fourier Transform in the West (FFTW) library.

The notion of discrete Fourier transform can be extended to define the nonuniform discrete Fourier transform of a (\(d\)-dimensional) discrete signal. Given any discrete signal \(v : \Omega \to \mathbb{R}\), we call nonuniform discrete Fourier transform of \(v\) the complex signal \(\mathrm{NDFT}(v) : \mathbb{R}^d \to \mathbb{C}\) defined by

(14)\[\forall \omega \in\mathbb{R}^d\,,\quad \mathrm{NDFT}(v)(\omega) = \sum_{k \in \Omega} v(k) \, e^{-i \langle k , \omega \rangle}.\]

The PyEPRI package relies on the Flatiron Institute Nonuniform Fast Fourier Transform (FINUFFT) library for the fast and accurate evaluation of the \(\mathrm{NDFT}\) operator over any sequence \(\omega = (\omega_1, \omega_2, \dots, \omega_M) \in (\mathbb{R}^d)^M\) made of \(M\) nonuniform frequency nodes (see [Bar21, BMaK19, SWA+21]).

Last, for any field gradient vector \(\gamma\in\mathbb{R}^d\), let us define the set

(15)\[C_{\delta, \delta_B}^{N_B}(\gamma) = \left\{\alpha \in \mathbb{Z}\,,\quad \|\alpha \, \gamma \| < \frac{N_B \delta_B}{2 \delta} \text{ and } | \alpha | < \frac{N_B}{2}\right\}\,.\]

Under several assumptions (see more details in [ABDF23]) we can derive the following approximation between the discrete Fourier coefficients of the discrete projection \(p_\gamma\), those of the discrete reference spectrum \(h_X\), and some nonuniform discrete Fourier coefficients of the discrete image \(u_X\), that is, for all \(\alpha \in I_{N_B}\),

(16)\[\begin{split}% \mathrm{DFT}(p_{X,\gamma})(\alpha) \approx \mathrm{DFT}(h_X)(\alpha) \cdot \left\{ % \begin{array}{cl} % \delta^d \cdot \mathrm{NDFT}(u_X)\left(-\frac{2 \pi \alpha \delta}{N_B \delta_B} \, \gamma\right) & \text{if } \alpha \in \mathcal{C}_{\delta, \delta_B}^{N_B}(\gamma) \\ % 0 & \text{otherwise.} % \end{array} \right.\end{split}\]

We are now ready to formally define the projection operator implemented in the PyEPRI package.

Single source operators

Projection operator

Neglecting the modeling and approximation errors involved in (16), we get

(17)\[p_{X,\gamma} = A_{X,\gamma}(u_X)\]

where \(A_{X,\gamma} u_X\) is defined through its discrete Fourier coefficients by setting, for all \(\alpha\in I_{N_B}\),

(18)\[\begin{split}\mathrm{DFT}(A_{X,\gamma}(u_X))(\alpha) = \mathrm{DFT}(h_X)(\alpha) \!\cdot\! \left\{ % \begin{array}{cl} % \delta^d \!\cdot\! \mathrm{NDFT}(u_X)\left(-\frac{2 \pi \alpha \delta}{N_B \delta_B} \, \gamma\right) & \text{if } \alpha \in \mathcal{C}_{\delta, \delta_B}^{N_B}(\gamma) \\ % 0 & \text{otherwise.} % \end{array} \right.\end{split}\]

Equation (17) (through Equation (18)) defines a linear operator \(A_{X,\gamma} : \mathbb{R}^\Omega \to \mathbb{R}^{I_{N_B}}\) that can synthesize a discrete projection \(p_{X,\gamma}\) from a discrete image \(u_X\).

Note: in the above description, we made explicit the parametrization of the \(A_{X,\gamma}\) operator by the magnetic field gradient \(\gamma\) but the operator is also implicitly parameterized by the discrete reference spectrum \(h_X\) and the sampling steps \(\delta_B\) and \(\delta\) since these parameters are involved in the formal definition of \(A_{X,\gamma}\).

Given a sequence made of N magnetic field gradient vectors \(\Gamma = (\gamma_1, \gamma_2, \dots, \gamma_N) \in (\mathbb{R}^d)^N\), we can stack the projections generated using each \(A_{X,\gamma_n}\) operator (for \(1 \leq n \leq N\)), in order to generate a sinogram, leading to

(19)\[s_{X,\Gamma} := A_{X,\Gamma} (u_X) := \big(A_{X,\gamma_1}(u_X), A_{X,\gamma_2}(u_X), \dots, A_{X,\gamma_N}(u_X)\big)\,.\]

Equation (19) defines another (and more general) linear operator that can synthesize a discrete sinogram \(s_{X,\Gamma}\) from a discrete image \(u_X\).

PyEPRI implementation : the \(A_{X,\Gamma}\) operator is implemented in the pyepri.monosrc submodule of the PyEPRI package, more precisely in the pyepri.monosrc.proj2d() function (suited to 2D input images) and the pyepri.monosrc.proj3d() function (suited to 3D input images). Detailed and reproducible examples of use for the pyepri.monosrc.proj2d() and pyepri.monosrc.proj3d() functions are provided in the first two sections of this tutorial.

Backprojection operator

We call backprojection operator the adjoint \(A_{\Gamma}^*\) of the projection operator \(A_{\Gamma}\). For any sequence of magnetic field gradient vectors \(\Gamma = (\gamma_1, \gamma_2, \dots, \gamma_N) \in (\mathbb{R}^d)^N\) and any discrete sinogram \(s = (p_1, p_2, \dots, p_N) \in \left(\mathbb{R}^{I_{N_B}}\right)^N\) gathering \(N\) projections, it satisfies,

(20)\[A_{X,\Gamma}^* (s) = \sum_{n = 1}^{N} A_{X,\gamma_n}^* (p_n)\,,\]

and, from (18), one can easily check that, for any \(n \in \{1, 2, \dots, N\}\), the adjoint of \(A_{X,\gamma_n}\) (also called backprojection operator) satisfies

(21)\[\forall k \in \Omega\,,\quad A_{X,\gamma_n}^* (p_n)(k) = \frac{\delta^d}{N_B} \sum_{\alpha \in \mathcal{C}_{\delta,\delta_B}^{N_B}(\gamma_n)} \overline{\mathrm{DFT}(h_X)(\alpha)} \, \mathrm{DFT}(p_n)(\alpha) \, e^{- \frac{2 i \pi \alpha \delta}{N_B \delta_B} \, \langle \gamma_n ,\, k\rangle }\,,\]

where \(\overline{z}\) denotes the complex conjugate of \(z \in \mathbb{C}\). The sum over \(\alpha\) involved in (21) corresponds to the adjoint of the \(\mathrm{NDFT}\) transform of an image over the nonuniform frequency nodes

\[\omega \in \left\{- \frac{2 \pi \alpha \delta}{N_B \delta_B} \gamma_n\,,~~ \alpha \in \mathcal{C}_{\delta, \delta_B}^{N_B}(\gamma_n) \right\}\]

applied to the restriction to \(\mathcal{C}_{\delta, \delta_B}^{N_B}(\gamma_n)\) of the signal \(\overline{\mathrm{DFT}(h_X)} \cdot \mathrm{DFT}(p_n)\). It can be efficiently and accurately evaluated using the FINUFFT package.

PyEPRI implementation: the backprojection operator \(A_{X,\Gamma}^*\) is implemented in the pyepri.monosrc submodule of the PyEPRI package, more precisely in the functions pyepri.monosrc.backproj2d() (2D setting) and pyepri.monosrc.backproj3d() (3D setting). We refer to the two first sections of the dedicated tutorial for a detailed demonstration of theses functions.

Fast evaluation of a projection-backprojection operation

In this section, we focus on the projection-backprojection operation, that is, the evaluation of the discrete image \(v_X := A_{X,\Gamma}^* \circ A_{X,\Gamma} (u_X)\) from the discrete image \(u_X\) and for a given sequence of magnetic field gradient vectors \(\Gamma = (\gamma_1, \gamma_2, \dots, \gamma_N) \in (\mathbb{R}^d)^N\). Using (19) and (20), one easily gets

(22)\[ A_{X,\Gamma}^* \circ A_{X,\Gamma} (u_X) = \sum_{n = 1}^{N} A_{X,\gamma_n}^* \circ A_{X,\gamma_n} (u_X)\,.\]

In the following, we shall denote be \(\Upsilon\) the augmented image domain \(\Upsilon := I_{2 N_1} \times \dots \times I_{2 N_d}\) (recall that the image domain is \(\Omega = I_{N_1} \times \dots \times I_{N_d}\)). Besides, injecting (18) into (21), one easily gets,

(23)\[\forall k \in \Omega\,,\quad A_{X,\gamma_n}^* \circ A_{X,\gamma_n} (u_X)(k) = \sum_{k' \in \Omega} u_X(k') \, \varphi_{\gamma_n}(k-k')\]

where

(24)\[\forall k^{\prime\prime} \in \Upsilon\,,\quad \varphi_{\gamma_n}(k^{\prime\prime}) = \frac{\delta^{2d}}{N_B} \sum_{\alpha \in \mathcal{C}_{\delta, \delta_B}^{N_B}(\gamma_n)} \overline{\mathrm{DFT}(h_X)(\alpha)} \, \mathrm{DFT}(h_X)(\alpha) \, e^{-\frac{2 i \pi \alpha \delta}{N_B \delta_B} \langle k^{\prime\prime} , \, \gamma_n \rangle}\,.\]

Finally, using (23) into (22), we get

(25)\[ \forall k \in \Omega\,,\quad A_{X,\Gamma}^* \circ A_{X,\Gamma} (u_X) = \sum_{k' \in \Omega} u_X(k') \, \varphi(k-k') \quad \text{where}\quad \varphi := \sum_{n=1}^{N} \varphi_{\gamma_n}\,.\]

We can recognize in (25) a convolution between \(u_X\) and \(\varphi\) (notice that the two signals have different domains, since the domain of \(u_X\) is \(\Omega\) and is strictly included into \(\Upsilon\), the domain of \(\varphi\)). Also, this means that the \(A_{X,\Gamma}^* \circ A_{X,\Gamma}\) operator exhibits a Toeplitz structure. For that reason, the convolution kernel \(\varphi\) will be referred from now as a Toeplitz kernel. An efficient way to evaluate the convolution between \(u_X\) and the Toeplitz kernel \(\varphi\) consists in

extending by zero the signal \(u_X\) from its initial domain \(\Omega\) towards the augmented domain \(\Upsilon\),

computing the circular convolution (that is, the convolution with periodical boundary condition) between this augmented image and the kernel \(\varphi\),

and then cropping the resulting signal to the initial image domain \(\Omega\).

The circular convolution mentioned in step 2. of this process can be efficiently evaluated using Fast Fourier Transforms of the involved signals. This numerical trick is well known and usually more efficient (in terms of computation time) than a direct evaluation of the sum (25) thanks to the linear logarithmic complexity of the FFT Algorihtm. However, this process is also memory consuming due to the use of two signals with extended domain \(\Upsilon\), so that this trick may not be suited to images with too large dimensions \((N_1, \dots, N_d)\).

It is important to note that the evaluation of \(A_{X,\Gamma}^* \circ A_{X,\Gamma} (u_X)\) using the procedure described above is usually much more faster than the successive evaluation of the \(A_{X,\Gamma}\) and \(A_{X,\Gamma}^*\) operators taken separately (that is the evaluation of \(s_{X,\Gamma} = A_{X,\Gamma} (u_X)\) followed by the evaluation of \(v_X = A_{X,\Gamma}^* (s_{X,\Gamma})\)). The ability to rapidly perform the projection-backprojection operation is of crucial importance in the implementation of iterative algorithms dedicated to EPR imaging.

PyEPRI implementation: the PyEPRI package provides functions to compute the Toeplitz kernel \(\varphi\) and performing the fast evaluation of the projection-backprojection (22). The Toeplitz kernel \(\varphi\) can be computed using the function pyepri.monosrc.compute_2d_toeplitz_kernel() in the 2D setting and using the function pyepri.monosrc.compute_3d_toeplitz_kernel() in the 3D setting. Once the Toeplitz kernel is computed, the functions pyepri.monosrc.apply_2d_toeplitz_kernel() and pyepri.monosrc.apply_3d_toeplitz_kernel() can be used to evaluate efficiently the projection-backprojection \(A_{X,\Gamma}^* \circ A_{X,\Gamma} (u_X)\) in the 2D and 3D settings. Detailed examples of computation and use of Toeplitz kernels are available in the two first sections of this tutorial.

Multisources operators

Modeling

We will consider now a sample made of multiple EPR sources. We denote by \(\mathcal{X} = (X_1, X_2, \dots, X_K)\) the EPR sources contained into the sample to be imaged. We will again describe the projection process in the continuous domain before focusing on the discrete setting and the associated operators. For any \(j \in \{1,2,\dots, K\}\), let

\(h_{X_j}^c : \mathbb{R} \to \mathbb{R}\) denote the reference spectrum of the \(j\)-th EPR source \(X_j\);
\(U_{X_j}^c : \mathbb{R}^d \mapsto \mathbb{R}\) denote the concentration mapping of the \(j\)-th EPR source \(X_j\).

We shall also denote by \(U_{\mathcal{X}}^c := \big(U_{X_1}^c, U_{X_2}^c, \dots, U_{X_K}^c \big)\) the sequence gathering all mono-source concentration mappings.

In presence of a magnetic field gradient \(\gamma = \mu \cdot e_\theta \in \mathbb{R}^d\), the EPR projection acquired from the mixture \(\mathcal{X}\) of EPR sources is modeled as the signal \(P_{\mathcal{X},\gamma}^c : \mathbb{R} \to \mathbb{R}\) defined by

\[\forall B\in\mathbb{R}\,,\quad P_{\mathcal{X},\gamma}^c(B) = \sum_{j = 1}^{K} \big(h_{X_j}^c * \mathcal{R}_{\theta}^{\mu}(U_{X_j}^{c})\big)(B)\,,\]

According to this (linear) modeling, we can see that the projection \(P_{\mathcal{X},\gamma}^c\) is simply obtained by summing the contributions of all individual EPR sources.

Filtering and sampling the continuous signals as we did in the single-source framework yields their discrete counterparts, that are,

\(h_{X_j} : I_{N_B} \to \mathbb{R}\), the discrete reference spectrum associated to the \(j\)-th EPR source \(X_j\), that corresponds to the sampling of reference spectrum \(h_{X_j}^c\) (filtered by \(g_{\delta_B}\)) with sampling step \(\delta_B\);
\(u_{X_j} : \Omega_j \to \mathbb{R}\) the discrete concentration mapping of the \(j\)-th EPR source \(X_j\), corresponding to the sampling of the image \(U_{X_j}^c\) (filtered by \(f_\delta\)) with step \(\delta\) along each coordinate axis (where \(\Omega_j := I_{N_1^{(j)}} \times I_{N_2^{(j)}} \times \dots I_{N_d^{(j)}}\) represents the discrete domain with dimensions \((N_i^{(j)})_{1 \leq i \leq d}\) of the \(j\)-th EPR source image \(u_j\));
\(u_{\mathcal{X}} = \big(u_{X_1}, u_{X_2}, \dots, u_{X_K}\big)\), the sequence of discrete images gathering the discrete concentration mappings of all EPR sources present in the sample.

By summing the contributions of all different sources, we obtain the discrete projection \(p_{\mathcal{X},\gamma} : I_{N_B} \to \mathbb{R}\) defined by

(26)\[ p_{\mathcal{X},\gamma} = \sum_{j = 1}^K A_{X_j, \gamma}(u_{X_j})\,,\]

and that corresponds (up to modeling and approximation errors involved in the sampling process) to the sampling of \(\mathcal{P}_{\mathcal{X},\gamma}^c\) with sampling step \(\delta_B\) over the range \(B \in B_{cf} + \left[-\frac{B_{sw}}{2}, \frac{B_{sw}}{2}\right]\).

When a sequence \(\Gamma = \big(\gamma_1, \gamma_2,\dots, \gamma_N\big) \in \big(\mathbb{R}^d\big)^N\) of magnetic field gradient vectors is available, a discrete sinogram \(s_{\mathcal{X}, \Gamma} = (p_{\mathcal{X},\gamma_1}, p_{\mathcal{X},\gamma_2}, \dots, p_{\mathcal{X},\gamma_N}) \in (\mathbb{R}^{I_{N_B}})^N\) can be obtained using

(27)\[ s_{\mathcal{X},\Gamma} = \left( A_{\mathcal{X}, \gamma_1} (u_{\mathcal{X}}) , A_{\mathcal{X}, \gamma_2} (u_{\mathcal{X}}), \dots, A_{\mathcal{X}, \gamma_N} (u_{\mathcal{X}})\right)\,,\]

which simply stacks together the projections \(\left(A_{\mathcal{X}, \gamma_1}(u_{\mathcal{X}})\right)_{1 \leq n \leq N}\).

Projection operator

Equation (26) provides an explicit way to synthesize a projection from a sequence of multiple EPR sources. Formally, let us define the multisources projection operator \(A_{\mathcal{X},\gamma} : \mathbb{R}^{\Omega_1} \times \mathbb{R}^{\Omega_2} \times \dots \times \mathbb{R}^{\Omega_K} \to \mathbb{R}^{I_{N_B}}\) by

(28)\[\forall u = \big(u_1, u_2, \dots, u_K\big) \in \mathbb{R}^{\Omega_1} \times \mathbb{R}^{\Omega_2} \times \dots \times \mathbb{R}^{\Omega_K}\,,\quad A_{\mathcal{X},\gamma}(u) = \sum_{j = 1}^K A_{X_j, \gamma}(u_j)\,.\]

Considering now a sequence \(\Gamma = (\gamma_1, \gamma_2, \dots, \gamma_{N}) \in \big(\mathbb{R}^d\big)^N\) of field gradient vectors, the projection operator \(A_{\mathcal{X},\gamma}\) can be generalized into \(A_{\mathcal{X},\Gamma} : \mathbb{R}^{\Omega_1} \times \mathbb{R}^{\Omega_2} \times \dots \times \mathbb{R}^{\Omega_K} \mapsto (\mathbb{R}^{I_{N_B}})^N\) using, for any \(u = \big(u_1, u_2, \dots, u_K\big) \in \mathbb{R}^{\Omega_1} \times \mathbb{R}^{\Omega_2} \times \dots \times \mathbb{R}^{\Omega_K}\),

(29)\[A_{\mathcal{X},\Gamma}(u) = \left(A_{\mathcal{X},\gamma_1}(u) , A_{\mathcal{X},\gamma_2}(u) , \dots, A_{\mathcal{X},\gamma_N}(u) \right)\,.\]

The operator \(A_{\mathcal{X},\Gamma}\) can be used to generate a discrete sinogram from a sequence of multiple EPR source images.

PyEPRI implementation : the \(A_{\mathcal{X},\Gamma}\) operator is implemented into the pyepri.multisrc submodule of the PyEPRI package, more precisely in the pyepri.multisrc.proj2d() function (suited to sequences of 2D input images) and the pyepri.multisrc.proj3d() function (suited to sequences of 3D input images). Detailed and reproducible examples of use for the pyepri.multisrc.proj2d() and pyepri.multisrc.proj3d() functions are provided in the last two sections of this tutorial.

Backprojection operator

In the multisources setting, we call backprojection operator the adjoint \(A_{\mathcal{X},\Gamma}^*\) of the projection operator \(A_{\mathcal{X},\Gamma}\). We can show that, for any \(s = (p_1, p_2, \dots, p_N) \in (\mathbb{R}^{I_{N_B}})^N\), we have

(30)\[A_{\mathcal{X}, \Gamma}^* (s) = \sum_{n=1}^{N} A_{\mathcal{X}, \gamma_n}^* (p_n)\,,\]

where

(31)\[A_{\mathcal{X}, \gamma_n}^* (p_n) = \left( A_{X_1, \gamma_n}^* (p_n), A_{X_2, \gamma_n}^* (p_n), \dots, A_{X_K, \gamma_n}^* (p_n) \right) = \left( A_{X_m, \gamma_n}^* (p_n) \right)_{1 \leq m \leq K}\,,\]

is simply obtained by stacking the mono-source backprojection operators \(A_{X_j,\gamma_n}^*\) defined in Fourier domain in (21).

PyEPRI implementation: the multisources backprojection operator \(A_{\mathcal{X},\Gamma}^*\) is implemented in the pyepri.multisrc submodule of the PyEPRI package, more precisely in the functions pyepri.multisrc.backproj2d() (2D setting) and pyepri.multisrc.backproj3d() (3D setting). We refer to the two last sections of the dedicated tutorial for a detailed demonstration of theses functions.

Fast evaluation of a projection-backprojection operation

Let us focus on the projection-backprojection operation in the multisources setting. Let \(u = (u_1, u_2, \dots, u_K) \in \mathbb{R}^{\Omega_1} \times \mathbb{R}^{\Omega_2} \times \dots \times \mathbb{R}^{\Omega_K}\), let \(\Gamma = (\gamma_1, \gamma_2, \dots, \gamma_N) \in (\mathbb{R}^d)^N\). Thanks to (29) and (30), we have

(32)\[A_{\mathcal{X},\Gamma}^* \circ A_{\mathcal{X},\Gamma}(u) = \sum_{n = 1}^N A_{\mathcal{X},\gamma_n}^* \circ A_{\mathcal{X},\gamma_n}(u)\,.\]

Besides, from (28), (29) and (31), for any \(n \in \{1, 2, \dots, N\}\), we have

(33)\[A_{\mathcal{X},\gamma_n}^* \circ A_{\mathcal{X},\gamma_n}(u) = \left( \sum_{j = 1}^K A_{X_m, \gamma_n}^* \circ A_{X_j, \gamma_n}(u_j)\right)_{1 \leq m \leq K}\,.\]

Then, using (18) and (21), one gets,

(34)\[\forall k\in\Omega\,,\quad \left(A_{X_m, \gamma_n}^* \circ A_{X_j, \gamma_n}(u_j)\right)(k) = \sum_{k'\in\Omega} u_j(k') \, \psi_{m,j,\gamma_n}(k-k')\,,\]

where, for all \(k^{\prime\prime} \in \Upsilon\), we have set

(35)\[\psi_{m,j,\gamma_n}(k^{\prime\prime}) = \frac{\delta^{2d}}{N_B} \sum_{\alpha \in C_{\delta,\delta_B}^{N_B}(\gamma_n)} \overline{\mathrm{DFT}(h_{X_m})(\alpha)} \, \mathrm{DFT}(h_{X_j})(\alpha) \, e^{-\frac{2 i \pi \alpha \delta}{N_B \delta_B} \langle k^{\prime\prime} , \gamma_n \rangle}\,.\]

Using (34) into (33) and then into (32), we end up with

(36)\[ \forall k\in\Omega\,,\quad A_{\mathcal{X},\Gamma}^* \circ A_{\mathcal{X},\Gamma}(u)(k) = \left( \sum_{j = 1}^{K} \sum_{k'\in\Omega} u_j(k') \, \psi_{m,j}(k-k') \right)_{1 \leq m \leq K}\]

where \(\psi_{m,j}\) is defined by

(37)\[\psi_{m,j} = \sum_{n=1}^{N} \psi_{m,j,\gamma_n}\]

and will be referred as the Toeplitz kernel of the cross sources \((m,j)\). The cross sources Toeplitz kernels \(\left(\psi_{m,j}\right)_{1 \leq (m,j) \leq K}\) can be efficiently evaluated using the FINUFFT package.

Each term \(\sum_{k'\in\Omega} u_j(k') \, \psi_{m,j}(k-k')\) in (36) corresponds to the convolution between the \(j\)-th source image \(u_j\) and the kernel \(\psi_{m,j}\) defined in (37). Again, such convolution operation can be evaluated efficiently (using circular convolutions) provided by we extend by zero the signal image \(u_j\) over the augmented domain \(\Upsilon_j := I_{2 N_1^{(j)}} \times I_{2 N_2^{(j)}} \times \dots \times I_{2 N_d^{(j)}}\), allowing finally the fast evaluation of \(A_{\mathcal{X},\Gamma}^* \circ A_{\mathcal{X},\Gamma}(u)\) using \(K^2\) convolutions.

PyEPRI implementation: the PyEPRI package provides functions to compute the cross sources Toeplitz kernels \(\left(\psi_{m,j}\right)_{1 \leq (m,j) \leq K}\) and performing the fast evaluation of the projection-backprojection (32). The cross sources Toeplitz kernels \(\left(\psi_{m,j}\right)_{1 \leq i,j \leq K}\) can be computed using the function pyepri.multisrc.compute_2d_toeplitz_kernels() in the 2D setting and using the function pyepri.multisrc.compute_3d_toeplitz_kernels() in the 3D setting. Once the cross sources Toeplitz kernels are computed, the functions pyepri.multisrc.apply_2d_toeplitz_kernels() and pyepri.multisrc.apply_3d_toeplitz_kernels() can be used to evaluate efficiently the projection-backprojection \(A_{\mathcal{X},\Gamma}^* \circ A_{\mathcal{X},\Gamma} (u_X)\) in the 2D and 3D settings. Detailed examples of computation and use of Toeplitz kernels are available in the two last sections of this tutorial.